잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -
현록의 기록저장소
컴퓨터 구조 및 설계 - Chapter 3. Arithmetic for Computers 본문
Chapter 3. Arithmetic for Computers
ㆍArithmetic operations를 이해할 수 있다.
3.1 - Introduction
3.2 - Addition and Subtraction
3.3 - Multiplication
3.4 - Division
3.5 - Floating Point
3.6 - Parallelism and Computer Arithmetic: Subword Parellelism
3.7 - Real Stuff: Streaming SIMD Extensions and Advanced Vector Extensions in x86
3.8 - Going Faster: Subword Parallelism and Matrix Multiply
3.9 - Fallacies and Pitfalls
3.10 - Concluding Remarks
(목차를 블록 선택 후, Ctrl+F로 탐색 가능 - 브라우저에 따라 다를 수 있음)
<3.1 - Introduction>
Arithmetic for Computers
컴퓨터를 위한 산술
*정수(integer) 영역의 작업(operation)
ㆍ덧셈(Addition)과 뺄셈(Subtraction)
ㆍ곱셈(Multiplication)과 나눗셈(division)
ㆍ오버플로우(overflow)를 주의해야 함
*부동 소수점(floating-point)의 실수(real numbers)
ㆍ표현(representation)과 작업(operation)
<3.2 - Addition and Subtraction>
Integer Addition
정수형 덧셈
ㆁ예시: 7(0b111) + 6(0b110) = 13(0b1101)
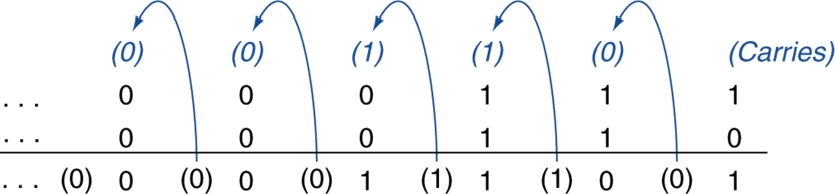
ㆁ만약 결과가 정수형 표현 가능한 범위를 벗어나면 오버플로우(overflow)가 일어남.
*피연산자가 양의 값(+ve)과 음의 값(-ve)인 덧셈에서는 오버플로우가 발생하지 않는다.
모든 수식을 세분화하면 항상 두 값의 연산으로 나뉘어짐.
피연산자도 정수형 표현 범위 내의 값일텐데, 어떤 경우에서도 정수형 범위 안의 결과를 얻음.
*피연산자 2개 모두 양의 값(+ve)이라면, 발생할 수도 있음.
ㆍ부호비트(MSB)로 1이 넘어가면서 음수화.
*피연산자 2개 모두 음의 값(-ve)이라면, 발생할 수도 있음(언더플로우, underflow).
ㆍ부호비트(MSB)가 1에서, 1이 넘어오면서 0이 되어 양수화.
Integer Subtraction
정수형 뺄셈
ㆁ2번째 피연산자(operand)가 음의 값인 덧셈처럼 비트 계산.
*2번째 피연산자를 음수로 만들고 비트덧셈.
ㆁ예시: 7 - 6 = 7 + (-6) = 1
+7: 0000 0000 .... 0000 0111
-6: 1111 1111 .... 1111 1010
───────────────
-1: 0000 0000 .... 0000 0001
ㆁ만약 결과가 정수형 표현 가능한 범위를 벗어나면 오버플로우(overflow)가 일어남.
*피연산자가 모두 양의 값(+ve)이거나, 모두 음의 값(-ve)이라면 오버플로우가 발생하지 않는다.
(각각 +-의 덧셈 혹은 -+의 덧셈이므로, 표현 범위 내의 값의 차이는 표현 가능한 범위 안의 결과임.)
*양의 값(+ve)에서 음의 값(-ve)을 뺀다면(+에+), 발생할 수도 있음.
ㆍ부호비트(MSB)로 1이 넘어가면서 음수화.
*음의 값(-ve)에서 양의 값(+ve)을 뺀다면(-에-), 발생할 수도 있음(언더플로우, underflow).
ㆍ부호비트(MSB)가 1에서, 1이 넘어오면서 0이 되어 양수화.
Dealing with Overflow
오버플로우 처리
ㆁ몇몇 언어(e.g., C)에서는 오버플로우를 무시한다(일어나도 그 값으로 둔다).
*MIPS instruction에서는 addu, addui, subu가 무시.
ㆁ다른 언어(e.g., Ada, Fortran)는 예외를 발생(raise an exception)시킨다.
*MIPS instruction에서는 add, addi, sub가 예외발생시킴.
*오버플로우가 발생하면, exception handler를 호출(invoke)한다.
ㆍPC(Program Counter)를 exception program counter(EPC) 레지스터에 저장한다.
ㆍ미리 정의된(predefined) handler의 주소로 점프한다.
ㆍmfc0 (coprocessor 레지스터로부터 move) instruction은
수정 조치(corrective action) 후에 return하기 위해
EPC의 값을 찾아낼 수 있다.
ㆍ(더 자세히는 Chapter 4 - The Processor에서 다룸)
Arithmetic for Multimedia
멀티미디어를 위한 산술
ㆁgraphics와 media는 8-bit와 16-bit 데이터의 벡터(vector) 기반 작업을 수행한다.
*분할된(partitioned) carry chain으로 작업한다. 64-bit adder를 사용한다면, 총합이 64-bit.
ㆍ8*8-bit, 4*16-bit, 2*32-bit 벡터에서 operation
*SIMD(Single-Instruction, Multiple-Data). 하나의 instruction으로 여러개의 데이터 처리.
ㆁSaturating operations
*오버플로우가 발생한다면, 결과는 표현가능한 범위에서 가장 큰 값이 된다(넘치진 않고 MAX에서 멈춘다).
ㆍc.f., 2s-complement modulo arithmetic
*e.g., 오디오의 clipping, 비디오의 saturation(채도)
<3.3 - Multiplication>
Multiplication
곱셈
*product 길이와 같은 긴 multiplicand로부터 시작
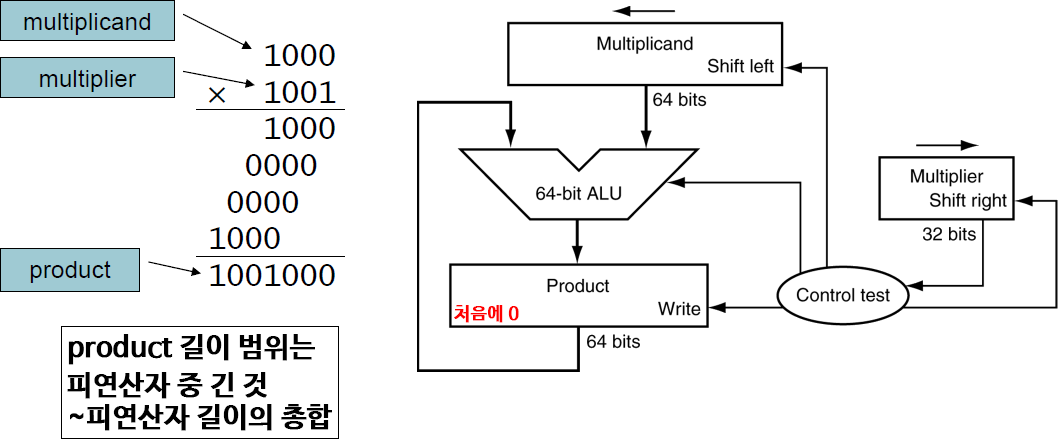
*초기 버전의 문제는, ALU가 64-bit.
ㆍ32-bit 두 수를 곱하는데 64-bit ALU를 사용
ㆍMultiplicand도 64-bit
Multiplication Hardware (First version)
하드웨어에서 곱셈 동작 (초기 버전)
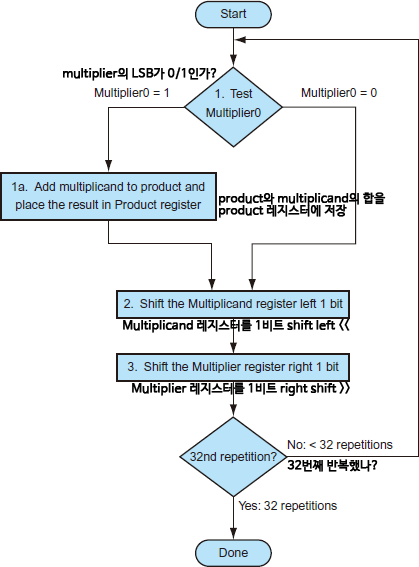
Optimized Multiplier (Sequencial version)
최적화된 곱셈기 (순차적인 버전)
*병렬(parallel)로 단계를 수행한다: add/shift

*partial-product에 더할 때마다 하나의 싸이클이 진행된다.
ㆍ그래도 괜찮다. 곱셈 주기(frequency)가 적다면.
Add and Right Shift Multiplier Hardware
덧셈과 오른쪽 쉬프트의 반복을 통한 곱셈기
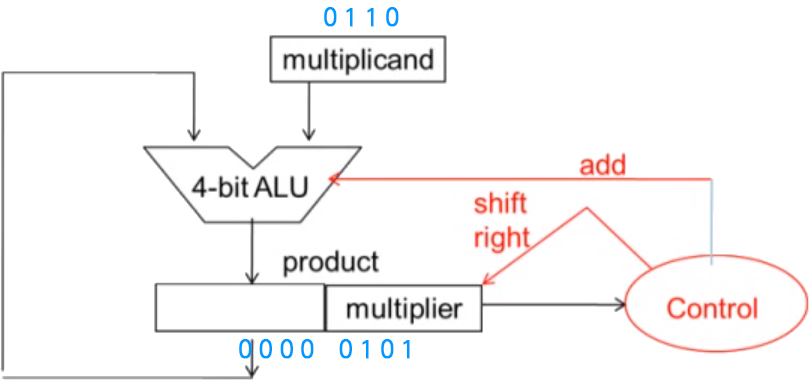
간단히 설명하기 위해, 4-bit 두 수를 곱하는 예시.
(ALU와 multiplicand 모두 4-bit. product는 8-bit.)
처음에 product의 하위 4비트에 multiplier로 채워진 채 시작.
(상위 4비트는 0)
multiplicand = 0b0110 (=6)
product = 0b0000 0101 (=5)
처음 0 0 0 0 0 1 0 1
add 0 1 1 0 0 1 0 1
shift 0 0 1 1 0 0 1 0
add 0 0 1 1 0 0 1 0 그대로 내려옴
shift 0 0 0 1 1 0 0 1
add 0 1 1 1 1 0 0 1
shift 0 0 1 1 1 1 0 0
add 0 0 1 1 1 1 0 0 그대로 내려옴
shift 0 0 0 1 1 1 1 0
4-bit 수의 곱셈이라, add/shift가 4단계 일어나면 종료한다.
결과는 0b0001 1110인 30.
Faster Multiplier
더 빨라진 곱셈기
*위의 sequncial version은, 4-bit의 수를 곱하려면 4번의 반복을 필요로 했음.
(32-bit의 수라면 32번의 반복)
*여러 개의 adder를 사용한다
ㆍcost/performance 교환.
결과를 빨리 얻을 수 있지만(성능은 높지만), 하드웨어를 많이 사용하므로 비용이 많이 든다.
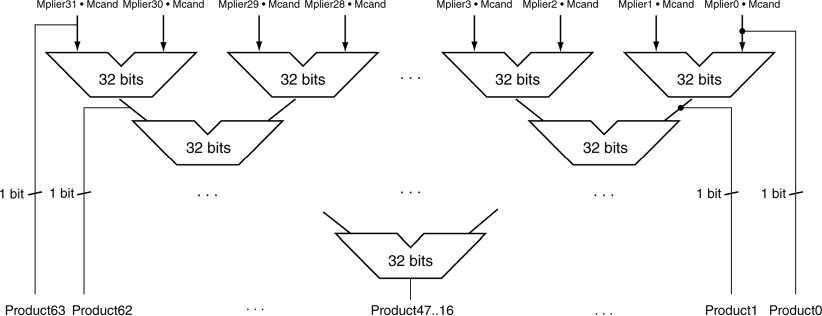
*pipeline화 가능하다(Chapter 4)
ㆍ각각의 곱 행동을 병렬적(parallel)으로 수행한다. 이러면 적은 하드웨어 리소스로도 빠른 연산(높은 throughput)이 가능하다.
MIPS Multiplication
MIPS 곱셈
ㆁproduct에 2개의 32-bit 레지스터를 사용한다. (결과는 64-bit으로 저장되기 때문에)
*HI: most-significant 32 bits. 상위 32비트.
*LO: least-significant 32 bits. 하위 32비트.
ㆁInstructions
*mult rs, rt / multu rs, rt
ㆍHI와 LO로 64-bit의 product를 생산(곱한다)
*mfhi rd / mflo rd
ㆍHI/LO로부터 rd로 move
ㆍ만약 product가 32 bits 보다 커서 오버플로우가 될지 HI의 값을 미리 보려고 할 때에 사용할 수 있다.
*mul rd, rs, rt
ㆍproduct의 하위 32비트를 rd로.
mult나 multu가 64비트 결과라면, mul은 32비트 결과.
<3.4 - Division>
Division
나눗셈
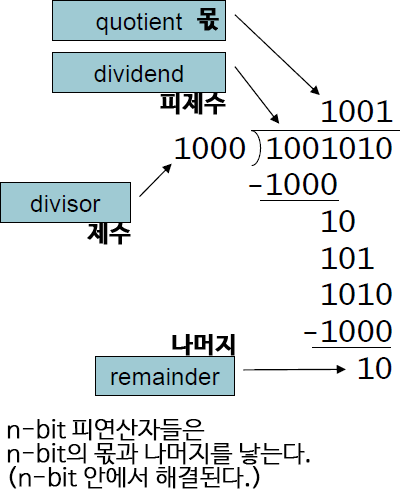
ㆁdivisor(제수, 나누는 수)가 0인지 확인한다.
ㆁ긴 나눗셈의 접근법
*현재까지의 dividend 자릿수가 divisor 자릿수보다 크거나 같다면,
ㆍ몫의 현재 비트에 1을 넣고, dividend에서 divisor만큼 뺀다.
*그렇지 않다면,
ㆍ몫의 현재 비트에 0을 넣고, dividend의 비트자리를 한단계 뒤로 추가한다(bring down next dividend bit).
ㆁRestoring(복원) division
*dividend에서 divisor만큼 뺐는데 음수가 된다면, 다시 divisor를 더해서 복원해줘야 한다.
ㆁSigned(부호) division
*절대값(부호없는)을 써서 나눗셈을 해야한다.
*그리곤 몫과 나머지의 부호를 조정해야 한다.
Division Hardware (First version)
나눗셈 하드웨어 (초기 버전)
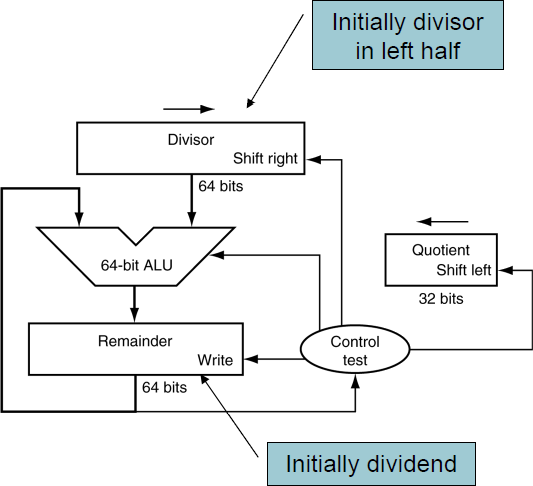
곱셈기의 초기버전처럼
64-bit의 ALU와 64-bit의 Divisor가 사용됨.
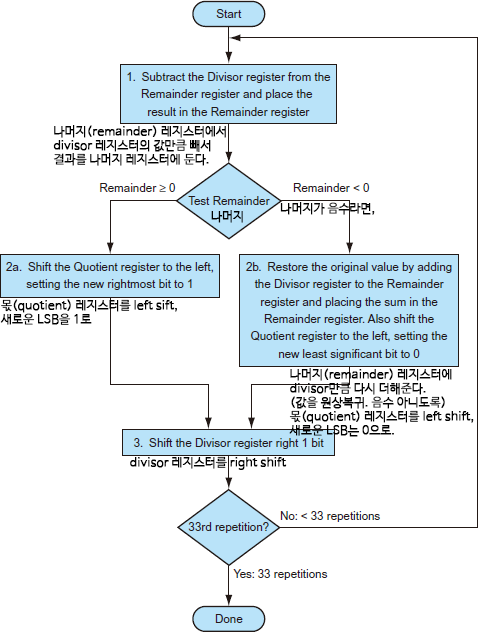
Optimized Divider (Sequencial version)
최적화된 나눗셈기 (순차적인 버전)
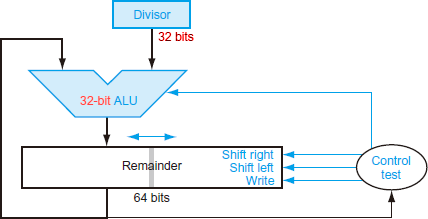
*partial-remainder에 뺄 때마다 하나의 싸이클이 진행된다.
*곱셈기와 닮은 부분이 많이 보인다.
ㆍ하드웨어적으로 양 쪽 연산 모두에 사용할 수 있다.
Left Shift and Subtract Division Hardware
왼쪽 쉬프트와 뺄셈을 통한 나눗셈기

간단히 설명하기 위해, 4-bit 두 수를 나누는 예시.
(ALU와 divisor 모두 4-bit. dividend는 8-bit.)
8-bit인 dividend는
상위 4비트가 remainder(나머지)로, 하위 4비트가 quotient(몫)로 작동한다.
(8-bit 레지스터에 초기값이 상위는 0들이고 하위는 dividend로 시작할 뿐..)
divisor = 0b0010 (=2)
dividend = 0b0000 0110 (=6)
처음 0 0 0 0 0 1 1 0
shift 0 0 0 0 1 1 0 0
sub 1 1 1 0 1 1 0 0
복구 0 0 0 0 1 1 0 0
shift 0 0 0 1 1 0 0 0
sub 1 1 1 1 1 0 0 0
복구 0 0 0 1 1 0 0 0
shift 0 0 1 1 0 0 0 0
sub 0 0 0 1 0 0 0 1
shift 0 0 1 0 0 0 1 0
sub 0 0 0 0 0 0 1 1
4-bit 수의 나눗셈이라, shift/sub가 4단계 일어나면 종료한다.
결과는 몫이 0b0011인 3. 나머지는 0.
Faster Divider
더 빨라진 나눗셈기
*multiplier처럼 병렬적(parallel)인 하드웨어를 사용할 수 없다.
ㆍ나눗셈에서는 remainder에 divisor를 뺀(subtraction) 결과가 음수인지 아닌지에 따라 다르게 동작하므로
여러 개의 하드웨어가 병렬적으로 처리할 수 없다.
*더 빠른 나눗셈기(e.g., SRT division)는 단계마다 동시에 여러 개의 quotient(몫) 비트를 구할 수 있다.
ㆍSRT division은 새로운 알고리듬
ㆍ그래도 여전히 여러 번의 단계는 필요하다.
MIPS Division
MIPS에서 나눗셈
ㆁ결과용으로 HI/LO의 2개의 레지스터를 사용한다.
*HI: 32-bit의 remainder(나머지)
*LO: 32-bit의 quotient(몫)
ㆁInstructions
*div rs, rt / divu rs, rt
*오버플로우는 발생하지 않는지, 0으로 나누는지(divide-by-zero) 확인한다.
ㆍ필요하다면 소프트웨어 단계에서 체크할 수도 있고..
*결과에 접근(access)하기 위해 mfhi, mflo 를 사용한다.
잠깐 복습,
Overflow의 정의는??
Result is out of range.
결과가 범위를 벗어난 것.
<3.5 - Floating Point>
Floating Point
부동소수점
*정수가 아닌 수(실수)를 표현하기 위해서.
ㆍ아주 작은 수(0.000...)나 아주 큰 수를 포함하여.
*scientific notation
(정수부가 일의 자리인 표현을 정규화된(normalized) 표현, 아니면 not normalized scientific notation.)
ㆍ-2.34 * 10^56 (normalized) = -2.34e56
ㆍ0.002 * 10^(-4) (not normalized) = 2.0e-7
ㆍ987.02 * 10^9 (not normalized) = 9.8702e11
*binary로는
ㆍ±1.xxxxxxx_2 * 2^(yyyy)
*C언어에서 float형과 double형이라는 타입이 있음.
Floating Point Standard
*IEEE(전기전자기술자협회)에 의해 IEEE 754로 정의됨
ㆍhttps://en.wikipedia.org/wiki/IEEE_754
ㆍhttps://ko.wikipedia.org/wiki/IEEE_754
*표현하는 방식이 많아지게 되자 개발됨
ㆍscientific code의 이식성 문제를 해결하고자
*현재 대부분 보편적으로 채택하고 있음
*2개의 표현법
ㆍsingle-precision (단정도, 32-bit)
ㆍdouble-precision (배정도, 64-bit)
※ 그 외
ㆍhalf-precision: 16-bit
ㆍquadruple-precision: 128-bit
ㆍoctuple-precision: 256-bit
IEEE Floating-Point Format
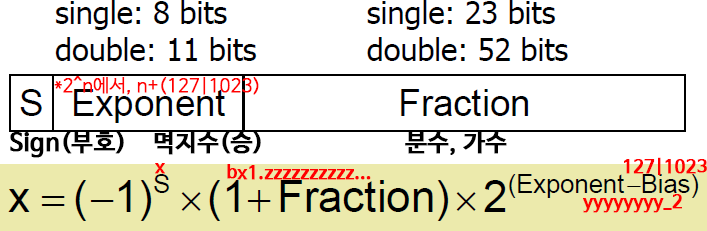
*-118.625_10을 예로 들면,
ㆍ음수이므로, 부호비트(MSB)는 1. 이제 절대값인 118.625로 볼 것.
ㆍ118.625_10은, 이진법으로는 1110110.101_2이며, (0.625 = 2^(-1)+2^(-3))
정규화시키면, 1.110110101*2^6_2 임.
ㆍ승(멱지수)인 6에 bias(IEEE 754에서 32-bit기준 127)을 더하면, 133이고, 이진법으로는 10000101_2.
ㆍ모든 부분을 비트로(32-bit, single-precision, float) 표현하면, 1 10000101 11011010100000000000000.
ㆍhttps://en.wikipedia.org/wiki/IEEE_754
ㆍhttps://ko.wikipedia.org/wiki/IEEE_754
*표현 규칙과 별개로(1.000... + 2^(-127)이 아닌), 모든 비트가 0이면 0.0000...을 표현함.
ㆍ(1*2^(-127)이 아주 작으니 데이터 상으로 0에 수렴해서 그럴 수도 있을 듯)
ㆍ좀 더 아래의 Denormal Numbers 파트에서 자세히.
*S: sign bit. 부호 비트. (양수는 0, 음수는 0)
*정규화된 significand: 이진법이므로, 1.0 ≤|significand|<2.0 (원래는 1.0~10.0)
ㆍ정수부는 항상 1비트이므로, 그 뒤만 기억(표기)하면 됨.
ㆍsignificand는 fraction에 숨겨진 "1."을 앞에 합치면 됨.
*exponent: 초과 표현(실제 exponent + bias).
ㆍexponent 비트는 unsigned 표현이다.
(즉, exponent는 1~2^(9|12)-1-1이고, 실제 멱지수는 1-(127|1023)~2^(9|12)-1-(127|1023)-1 이다.)
ㆍIEEE 754에서, single-precision의 bias는 127이고, double-precision의 bias는 1023.
Single-Precision Range
단정도 범위
*exponent(멱지수)는 00000001_2 이상 11111110_2 이하이다.
ㆍ00000000_2와 11111111_2는 사용되지 않는다(금지되어 있다).
*가장 작은 값(미세한 값. C++에서 .min() not .lowest())
ㆍexponent: 0b00000001
→ 실제 멱지수: 1-127 = -126
ㆍfraction: 000...000
→ significand = 0b1.0 = 1.0
ㆍ±1.0 * 2^(-126) ≒ ±1.1755e-38
*가장 큰 값
ㆍexponent: 0b11111110 (254)
→ 실제 멱지수: 254-127 = 127
ㆍfraction: 111...111
→ significand = 0b1.111...111 ≒ 1.9999998807907104 ≒ 2
ㆍ±2 * 2^(127) ≒ ±3.4028e38
Double-Precision Range
배정도 범위
*exponent(멱지수)는 00000000001_2 이상 11111111110_2 이하이다.
ㆍ00000000000_2와 11111111111_2는 사용되지 않는다(금지되어 있다).
*가장 작은 값(미세한 값. C++에서 .min() not .lowest())
ㆍexponent: 0b00000000001
→ 실제 멱지수: 1-1023 = -1022
ㆍfraction: 000...000
→ significand = 0b1.0 = 1.0
ㆍ±1.0 * 2^(-1022) ≒ ±2.2251e-308
*가장 큰 값
ㆍexponent: 0b11111111110 (4095)
→ 실제 멱지수: 2046-1023 = 1023
ㆍfraction: 111...111
→ significand = 0b1.111...111 ≒ 2
ㆍ±2 * 2^(1023) ≒ ±1.7977e308
Floating-Point Precision
ㆁRelative precision(상대적인 정도. 정확도.)
*모든 fraction(가수) 비트는 significant
*single: fraction이 23비트. 2^(-23)의 정확도.
ㆍ23 * log_10(2) ≒ 23 * 0.301 ≒ 6. 10진법 기준 소숫점 6자리까지.
*double: fraction이 52비트. 2^(-52)의 정확도.
ㆍ52 * log_10(2) ≒ 52 * 0.301 ≒ 16. 10진법 기준 소숫점 16자리까지.
*1/3 ≒ 0.333333 ≒ 0.3333333333333333
Floating-Point 예제 1
ㆁ-0.75를 표현
*-0.75 = (-1)^1 * (2^(-1)+2^(-2))
= (-1)^1 * 0b0.11
= (-1)^1 * 0b1.1 * 2^(-1)
*S = 1
*Fraction = 0b1000...000
*Exponent = -1 + bias
ㆍsingle: -1 + 127 = 126 = 0b01111110
ㆍdouble: -1 + 1023 = 1022 = 0b01111111110
ㆁsingle: 1 01111110 1000...000
ㆁdouble: 1 01111111110 1000...000
Floating-Point 예제 2
*single-precision float인 0b1 10000001 01000...000 가 십진수로 어떤 수인지.
ㆍS = 1
ㆍExponent = 0b100000001 = 129
→ 실제 exponent = 129 - 127 = 2
ㆍFraction = 0b01000...000
*x = (-1)^1 * 0b1.01 * 2^2
= (-1)^1 * (1 + 2^(-2)) * 2^2
= (-1)^1 * (1.25) * 4
= -5.0
Denormal Numbers
비정규 숫자
*exponent가 0b000...000 이라면,
fraction의 숨겨진 비트를 0으로 한다.
ㆍ원래 정규식 대로라면 fraction의 숨겨진 비트는 1.이고, 1.xxxx...이 된다.
ㆍ하지만 정규식에 금지된(000...000과 111...111) 비트 중 하나인 000...000에서는 숨겨진 비트를 0으로 본다.
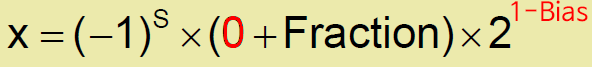
*표준에서의 범위보다 더 작은 값을 위해서.
ㆍ정도(precision)를 줄여서, 점진적으로 작은 값을 허용.
ㆍ2^(1-bias)는 고정이고, 숨겨진 비트도 0이므로, fraction 비트의 0.xxxx...에 값이 결정됨.
*여기서 fraction도 0b000...000이라면, 값은 딱 0.0이 될 수 있음.
ㆍx = ±1 * (0.00000000) * 2^(-126|-1022) = 0.0
Infinities and NaNs
무한대와 숫자가아님(Not-a-Number)
ㆁ이번엔 exponent가 금지된 비트 중 하나인 0b111...111
ㆁexponent = 0b111...111, fraction = 0b000...000
*±무한대. (부호비트에 따라)
*subsequent calculation에 사용될 수 있다. 오버플로우 강제 체크를 피하기 위해 사용된다??
ㆁexponent = 0b111...111, fraction ≠ 0b000...000
*숫자가 아님. Not-a-Number(NaN).
*illegal 혹은 undefined result
ㆍe.g., divided by zero
*subsequent calculation에 사용될 수 있다.
Floating-Point Addition
부동소수점 덧셈
*10진수 소숫점 4자리의 예시
ㆍ9.999e1 + 1.610e-1
1. 소숫점 정렬
ㆍ작은 수를 큰 수에 맞춤(작은 수를 조정).
ㆍ9.999 * 10^1 + 0.0161 * 10^1
2. significand끼리 더함
ㆍ9.999 + 0.0161 = 10.0151. 즉, 1.00151 * 10^1
3. 결과를 정규화하고, 오버플로우/언더플로우 하지 않았는지 검사
ㆍ1.0015 * 10^2. 1.0015e2
4. 필요하다면 반올림하거나 비정규화한다.
(ㆍ1.002e2, 10^2, 100)
*binary 소숫점 4자리의 예시
ㆍ1.000_2 * 2^(-1) + -1.110_2 * 2^(-2) = 0.5 + -0.4375
1. 소숫점 정렬
ㆍ작은 수를 큰 수에 맞춤(작은 수를 조정).
ㆍ1.000_2 * 2^(-1) + -0.1110_2 * 2^(-1)
2. significand끼리 더함
ㆍ01.000_2 + 11.001_2 = 00.001_2 = 0.001_2. 즉, 0.001_2 * 2^(-1)
3. 결과를 정규화하고, 오버플로우/언더플로우 하지 않았는지 검사
ㆍ1.000_2 * 2^(-4)
4. 필요하다면 반올림하거나 비정규화한다.
(ㆍ2^(-4), 0.0625)
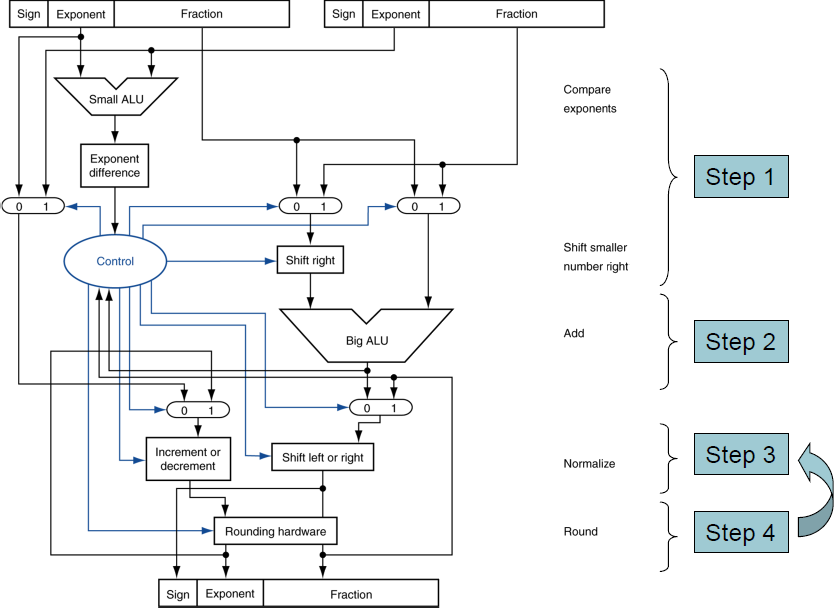
FP Adder Hardware
부동소수점 가산기
*integer adder(정수 가산기)보다 훨씬 더 복잡함.
*한 번의 clock cycle 안에 작업을 하기엔, cycle이 아주 오래 걸리게(느리게) 될 수 있음.
ㆍinteger operation보다 훨씬 느림.
ㆍ느린 clock은 전체 instruction들을 전체적으로 불리하게(느리게) 만듦.
*그러므로, FP adder는 일반적으로 여러 번의 cycle로 동작한다.
ㆍpipeline화(병렬적으로) 될 수 있다.
ㆍ하나의 명령에는 여러 cycle이 걸리지만,
throughput을 높여 여러 개의 명령어를 동시에 실행하므로,
단위 시간당 FP adder의 가능한 작업의 수는 증가.
Floating-Point Multiplication
부동소수점 곱셈
*10진수 소숫점 4자리의 예시
ㆍ1.110e10 + 9.200e-5
1. exponent끼리 더함
ㆍ새로운 멱지수 = 10 + -5 = 5
2. significand끼리 곱함
ㆍ1.110 * 9.200 = 10.212. 즉, 10.212e5
3. 결과를 정규화하고, 오버플로우/언더플로우 하지 않았는지 검사
ㆍ1.0212e6
4. 필요하다면 반올림하거나 비정규화한다.
(ㆍ1.021e6)
5. 피연산자들의 부호로부터, 결과 부호를 결정
ㆍ+1.021e6
*binary 소숫점 4자리의 예시
ㆍ1.000_2 * 2^(-1) + -1.110_2 * 2^(-2) = 0.5 * -0.4375
1. exponent끼리 더함
ㆍbias 없이: -1 + -2 = -3
ㆍbias가 이미 적용된: (-1 + 127) + (-2 + 127) -127 = -3 + 254 - 127 = -3 + 127. (비트에 들어갈)
2. significand끼리 곱함
ㆍ1.000_2 *(비트OR) 1.110_2 = 1.110_2. 즉, 1.110 * 2^(-3)
3. 결과를 정규화하고, 오버플로우/언더플로우 하지 않았는지 검사
ㆍ1.110_2 * 2^(-3)
4. 필요하다면 반올림하거나 비정규화한다.
(ㆍ1.110_2 * 2^(-3), 0.21875)
5. 피연산자들의 부호로부터, 결과 부호를 결정 (+ve * -ve → -ve)
ㆍ-1.110_2 * 2^(-3), -0.21875
FP Arithmetic Hardware
부동소수점 산술 하드웨어
*FP multiplier(곱셈기)의 복잡도는 FP adder(가산기)와 비슷하다(비슷하게 복잡하다).
ㆍ하지만 adder에서는 significand끼리 더했지만, multiplier는 곱한다.
*FP 산술 하드웨어는 보통 다음 기능들을 지원한다.
ㆍAddition(덧셈), Subtraction(뺄셈), Multiplication(곱셈), Division(나눗셈), Reciprocal(역수, 분모), Squareroot(제곱), ...
ㆍFP↔integer 변환(conversion)
*FP operation은 일반적으로 여러 번의 cycle로 동작한다.
ㆍpipeline화(병렬적으로) 될 수 있다.
FP Instructions in MIPS
MIPS의 부동소수점 명령어
FP 예제 1: ℉ to ℃
화씨(Fahrenheit)에서 섭씨(Celcius)로
FP 예제 2: Array Multiplication
배열 곱셈
Accurate Arithmetic
정확한 산술계산
<3.6 - Parallelism and Computer Arithmetic: Subword Parellelism>
Subword Parallellism
subword 병렬처리
<3.7 - Real Stuff: Streaming SIMD Extensions and Advanced Vector Extensions in x86>
x86 FP Architecture
x86 FP Instructions
Streaming SIMD Extension 2 (SSE2)
<3.8 - Going Faster: Subword Parallelism and Matrix Multiply>
Matrix Multiply
<3.9 - Fallacies and Pitfalls>
Right Shift and Division
Associativity
연관성
Who Cares About FP Accuracy?
어느 분야에서 부동소수점의 정확도가 중요한가?
<3.10 - Concluding Remarks>
Concluding Remarks
끝맺으며
111 ㆁ * ㆍ ※→←↑↓↔↕±≒≠111
'Study > Computer Science' 카테고리의 다른 글
| 컴퓨터 구조 및 설계 - Chapter 5. Large and Fast: Exploiting Memory Hierarchy (1) | 2019.12.24 |
|---|---|
| 컴퓨터 구조 및 설계 - Chapter 4. The Processor (7) | 2019.12.15 |
| 컴퓨터 구조 및 설계 - Chapter 2. Instructions: Language of the Computer (5) | 2019.11.30 |
| 컴퓨터 구조 및 설계 - Chapter 1. Computer Abstractions and Technology (0) | 2019.11.28 |
| 컴퓨터 구조 및 설계 - 하드웨어/소프트웨어 인터페이스 (0) | 2019.11.28 |
잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -




