잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -
현록의 기록저장소
[Lv4] 스마트한 프로도 본문
https://programmers.co.kr/learn/challenges
프로그래밍 강의 | 프로그래머스
기초부터 차근차근, 직접 코드를 작성해 보세요.
programmers.co.kr
문제 설명
스마트한 프로도

직장인 프로도는 오늘도 열심히 일한다. 회사에서 인정받는 프로도는 직장 상사에게 문제를 풀어 달라는 요청을 받았다. 문제를 읽은 프로도는 혼자 풀긴 어려운 문제로 보여 여러분에게 도움을 요청하였다. 상사가 전달한 문제는 아래와 같다.
그래프 G에 대해서, 서로 다른 두 정점 사이에 간선이 존재한다면 단지 한 간선만 존재한다. 또한 동일한 정점을 연결하는 간선(셀프 루프)은 존재하지 않는다. G의 두 간선 e_1과 e_2가 인접하다면, e_1이 연결하는 두 정점 중 하나는 e_2가 연결하는 정점과 일치한다. 그래프 G의 매칭 M은 간선들의 집합이고 M에 속하는 임의의 두 간선은 서로 인접하지 않다. 여기서, 공집합은 매칭임에 주목하자.
그래프 G와 정수 k에 대해서, 초기에 |M_0|≥k이고 |M_t|≥k 인 두 매칭 M_0와 M_t가 주어진다. 우리는 매칭 M_0에서 G의 간선을 추가하거나 또는 삭제해서 M_0를 변환한다. 변환의 한 단계에서는 하나의 간선을 추가하거나 삭제할 수 있다. 이렇게 해서 변환된 간선들의 집합 M_1은 다시 매칭이 되어야 한다. 다시 말해서, 각 변환 단계의 결과물은 매칭이어야 한다. 따라서 i번째 단계에서는 매칭 M_i-1를 매칭 M_i로 변환하게 된다.
이런 식으로 M_0에서 시작해서 중간 매칭들로의 변환 단계들을 거쳐서 마지막에 M_t를 만들어야 한다. 다시 말해서, p번의 단계를 거쳐 만들어진 매칭 M_p에 대해서, M_p = M_t를 만족하면 된다. 하지만 중간에 만들어지는 M_i (0 < i < p)는 크기에 제한이 있어서 |M_i| ≥ k-2를 만족해야만 한다.
매칭 M_0에서 M_t로 위의 조건들을 만족하면서 항상 변환할 수 있다는 것이 잘 알려져 있다. 따라서 여러분은 그 변환 과정을 리턴하는 프로그램을 작성하여야 한다.
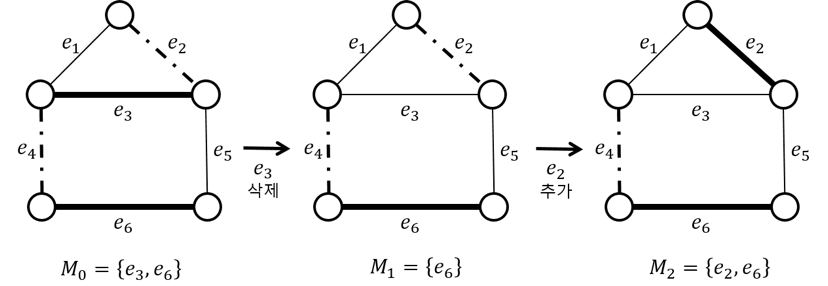
예를 들어, 아래 그림에서 초기 매칭 M_0 = {e_3, e_6}이고 마지막 매칭 M_t = {e_2, e_4}이고, k = 2 인 경우이다. 그림에서와 같이 간선들을 추가하거나 삭제하면, M_0에서 M_t로 변환할 수 있다.

입력 형식
입력은 총 9가지의 변수로 주어진다. n과 m은 각각 그래프 G의 정점과 간선의 수이다. 그래프 G의 정점들은 1부터 n까지의 정수로, 간선들은 1부터 m까지의 정수로 나타낸다. a와 b는 각각 크기가 m인 1차원 배열로, 간선이 잇는 두 점을 나타낸다. i번째 간선이 잇는 두 정점의 번호가 a와 b의 i번째 원소가 된다. k는 문제에서 설명된 것과 같다. m1과 m2는 각각 초기 매칭 M_0의 크기, 마지막 매칭 M_t의 크기이다. e1과 e2는 각각 M_0와 M_t에 속하는 간선의 정보를 나타내는 1차원 배열이며, 각각의 원소의 개수는 m1과 m2이다. 제한조건은 다음과 같다.
- 1 <= n <= 100,000
- 1 <= m <= 1,000,000
- 1 <= k <= 50,000
- m1 >= k, m2 >= k
출력 형식
리턴 타입은 2차원 정수 배열이다. 매칭 M_0에서 M_t로 변환하는데 p단계가 걸린다고 할 때, 배열의 크기는 p × 2가 되어야 한다. 각 행의 첫 번째 원소는 0 또는 1로, 0이면 간선을 삭제했음을 의미하며 1이면 간선을 추가했음을 의미한다. 두 번째 원소는 추가 또는 삭제하는 간선의 번호이다. 답이 될 수 있는 변환이 여러 가지인 경우에는 그중 한 가지를 리턴하면 된다.
| 변수명 | 값 |
| n | 5 |
| m | 6 |
| a | [1, 1, 2, 2, 3, 4] |
| b | [2, 3, 3, 4, 5, 5] |
| k | 2 |
| m1 | 2 |
| m2 | 2 |
| e1 | [3, 6] |
| e2 | [2, 4] |
| answer | [[0, 3], [1, 2], [0, 6], [1, 4]] |
알림
이 문제의 경우 같은 입력에 대해 정답이 여러 개 존재할 수 있으나, ‘실행’을 눌러 예제 입출력에 대해 테스트를 진행할 때 등록된 한 가지 답만 정답으로 처리되고 있습니다. ‘코드 채점’을 눌러 제출할 시에는 올바르게 채점되니 참고하여 주시기 바랍니다.
이번 문제를 풀게된 이유는 간단하다.
이런거 보면 너무 궁금하잖아!!
엌ㅋㅋㅋ
문제 자체는 어렵지 않다. 노드를 잇는 문제들 느낌?
[Problem Solving/programmers] - [Lv3] 가장 먼 노드
획득 점수도 1로 낮다.
아마 사람들이 풀지 않은건 문제를 읽다가 귀찮아서 안풀어서 그런 듯 하다;;
딱히 어렵지도 않은걸 획득 점수 스스로도 알고있으니, 일부러 읽기 귀찮은 문제로 노린 듯 하다.
1. 한 점에서 다른 점으로 이어질 수도 있고, 아닐 수도 있음.(모든 점이 서로 이어진 것은 아님)
2. 점 사이를 잇는 다리(선)는 하나 뿐, 같은 위치에 겹치지 않음.
3. 선들의 집합에서 여러 선을 빼거나 더하면서 최종목표 집합과 같은 형태로 도달.
4. 선을 더할 때는 인접선이 집합에 이미 있으면 안 됨.(한 점을 여러번 쓸 수 없음)
5. 집합 안에 선의 갯수는 k-2개 이상인 채로는 유지하면서 빼거나 더해야함.(뺄 때 주의하면 됨.)
ArrayList<Dot> dots = new ArrayList<>();
for(int i=0;i<n;i++) dots.add(new Dot(i+1));
ArrayList<Line> lines = new ArrayList<>();
for(int i=0;i<a.length;i++) {
Line l = new Line(i, dots.get(Math.min(a[i], b[i])-1), dots.get(Math.max(a[i], b[i])-1));
lines.add(l);
}점을 기준으로 할까, 선을 기준으로 할까 하다가,
문제에서 선의 집합들을 최종목표에 도달시키는 것이니, 선으로 정했습니다.
선에 점의 정보가 들어가도록 할겁니다.
이 점들과 선들은 필요할 때 호출해서 쓸 것이므로, 번호 호출이 용이한 ArrayList에 각각 담았습니다.
class Dot {
int num;
boolean used;
Dot(int num) {
this.num = num;
this.used = false;
}
}
class Line {
int index;
Dot dot1;
Dot dot2;
Line(int index, Dot dot1, Dot dot2) {
this.index = index+1;
this.dot1 = dot1;
this.dot2 = dot2;
}
@Override
public int hashCode() {
return index;
}
@Override
public boolean equals(Object obj) {
return (this.hashCode()==obj.hashCode());
}
}선에는 스스로의 번호, 점 2개의 정보가 들어가고,
점에는 스스로의 번호, 내가 현재 사용 중인지의 boolean으로 구성했습니다.
진행하면서 사용할 선의 집합은 딱히 순서가 중요한게 아니라, 구성성분이 중요하니 빠른 HashSet으로 할겁니다.
그래서 혹시 모르니 hashCode와 equals를 오버라이딩 해뒀습니다.(굳이 중복으로 추가하려 하진 않습니다만)
구분정보는 자신의 번호가 고유하니까 그거면 될 듯하네요.
HashSet<Line> selected = new HashSet<>() {
public boolean equals(Object o) {
HashSet<Line> other = (HashSet)o;
boolean isSame = true;
if(this.size()!=other.size()) return false;
for(Line l:this) {
if(!other.contains(l)) {
isSame = false;
break;
}
}
return isSame;
};
};
for(int i=0;i<e1.length;i++) {
Line l = lines.get(e1[i]-1);
selected.add(l);
l.dot1.used = true;
l.dot2.used = true;
}
LinkedList<Line> toDo = new LinkedList<>();
HashSet<Line> must = new HashSet<>() {
public boolean equals(Object o) {
HashSet<Line> other = (HashSet)o;
if(this.size()!=other.size()) return false;
boolean isSame = true;
for(Line l:this) {
if(!other.contains(l)) {
isSame = false;
break;
}
}
return isSame;
};
};
for(int i=0;i<e2.length;i++) {
Line l = lines.get(e2[i]-1);
if(!selected.contains(l)) toDo.add(l);
must.add(l);
}
LinkedList<int[]> answer = new LinkedList<>();HashSet<Line> selected가 진행하면서 사용할 집합입니다.
처음 조건에 주어진 e1에 있는 Line은 전부 selected에 넣어주고, 해당하는 점들도 사용인 상태로 표시해줍니다.
LinkedList<Line> toDo는 새로 추가해야 할(selected에는 없지만 최종목표에는 있는) 선들입니다.
빼면서 진행할거라서 추가/제거에 더 나은 LinkedList로 만들었습니다.
HashSet<Line> must는 최종목표에 있는 모든 선들입니다.
selected에서 추가하거나 빼야하는데, 추가는 toDo를 기준으로 추가하면 되지만,
뺄 때는 혹시 기껏 넣어둔게 빠지면 안되므로, must에 있는 애들은 안빠지도록 기준으로 삼을겁니다.
HashSet은 진행하면서 사용할 집합과, 최종목표를 나타낼 것이고, 이 둘을 비교할 것이기 때문에
equals를 재정의합니다.
비교는 어차피 HashSet<Line>끼리만 비교한다면 casting으로 인한 예외는 없을 것이고,
사이즈가 같고, 자신의 모든 항목을 상대방도 가지고 있다면 같다고 판정합니다.
LinkedList<int[]> answer는 정답이 [[0-1],[\d]]형태의 배열들로 이루어지고,
크기도 모르므로, LinkedList를 만들어 계속 넣어줄겁니다.
while(true) {
if(selected.equals(must)) break;
Line forDel = null;
if (selected.size()>k-2) {
for(Line el:selected) {
if(!must.contains(el)) {
forDel = el;
break;
}
}
if(forDel!=null) {
answer.add(new int[] {0,forDel.index});
selected.remove(forDel);
forDel.dot1.used = false;
forDel.dot2.used = false;
}
}
Line forAdd = null;
for(Line nl:toDo) {
if(nl.dot1.used) break;
if(nl.dot2.used) break;
forAdd = nl;
break;
}
if(forAdd!=null) {
answer.add(new int[] {1,forAdd.index});
selected.add(forAdd);
toDo.remove(forAdd);
forAdd.dot1.used = true;
forAdd.dot2.used = true;
}
if(forDel==null&&forAdd==null) break;
}
int[][] answerarr = new int[answer.size()][2];
for(int i=0;i<answerarr.length;i++) answerarr[i] = answer.get(i);
return answerarr;맨 위 비교 부분(equals)은 처음에 생각하지 않습니다.
먼저 selected의 크기가 k-2보다 크면 한 개는 더 빼도 되겠죠. k-2이상의 크기를 유지하라고 했으니까.
selected의 선들 중, must에 없는 선은 최종목표에 필요없는 선이니 빼도 됩니다.
뺄게 있다면 빼줍니다.
toDo의 선들은 새로 추가해야 할 선들만 모여있습니다.
여기에서 선의 점 2개가 사용 중이지 않다는건 selected에 인접한 선이 없다는 것이므로 추가 가능합니다.
추가할 수 있는게 있다면 추가해주고, toDo에서도 제외시켜서 다음번에 중복되게 하지 않습니다.
이렇게 k-2이상의 크기를 유지하면서 필요없는 애들은 마구 버려주고(얘를 k-2이상인 while로 해도됩니다.),
toDo에 남은 선들 중 두 점이 사용 중이지 않은 애들은 넣어주고를 반복하면
최소의 단계로 최종목표까지 도달됩니다.(근데 문제는 굳이 최소단계일 필요는 없음)
단, 위의 최종 break에서 문제가 조금 있는데,
현재 몇몇 케이스는 이대로 통과가 되는데, 유독 코드 채점만 통과가 안됩니다.
HashSet끼리의 equals가 코드 채점만 먹히질 않고,
set의 사이즈가 같을 때 Iterator로 꺼내서 일일이 비교해도 break에 도달하질 못합니다.
그래서 forDel==null&&forAdd==null로 더 이상 지울 것도 없고(k-2 이상인 크기를 유지하면서 필요 없는 선이 없음),
더 이상 추가할 것도 없을 때(toDo를 이미 다 추가했거나, 점들이 이미 사용 중이라 추가를 못함)
그냥 더 돌지말고 나오라고 했더니 답이 됩니다..(?)
문제에서는 최종목표까지 항상 도달할 수 있다고 했습니다. 도달 가능한 조건만 주어지겠죠.
문제에서 주어진 e2를 도중에 바꿔서 (e2→e2')
정답 채점시에는 바뀐 e2'를 기준으로하여 제출한 배열로 선을 뺐다 더하면서 e2'에 도달하는지로 답을 매기는데,
호출시 e2는 그대로라, 우리는 e2를 받게 되고, e2는 도달이 불가능한 조건이고..
결국 할만큼 하다 빠져나와서 현재까지의 답을 제출했는데..
그 배열대로 진행하는게 e2'(아마 바꿀 때 이를 기준으로 바꿨다면)라서 통과는 되는..??
상태로 추측이 됩니다.
문제 풀이 자체는 그냥 노드의 선 잇기 정도와 유사한 난이도에 특별히 까다로운 조건도 없으니,
테스트 케이스나 다른 임의 예제가 먹히는 equals이 코드 채점에서만 안되는건 신경쓰지 않기로 하고 끝냈습니다.
'Problem Solving > programmers' 카테고리의 다른 글
| [Lv1] 신규 아이디 추천 (0) | 2021.04.12 |
|---|---|
| [Lv1] 두 개 뽑아서 더하기 (0) | 2021.04.12 |
| [Lv4] 지형 편집 (2) | 2019.04.30 |
| [Lv3] 보행자 천국 (0) | 2019.04.25 |
| [Lv3] 가장 먼 노드 (0) | 2019.04.25 |
잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -


