잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -
현록의 기록저장소
[Lv4] 지형 편집 본문
https://programmers.co.kr/learn/challenges
프로그래밍 강의 | 프로그래머스
기초부터 차근차근, 직접 코드를 작성해 보세요.
programmers.co.kr
문제 설명
XX 게임에서는 지형 편집 기능을 이용하여 플레이어가 직접 게임 속 지형을 수정할 수 있습니다. 이 게임에서는 1 x 1 x 1 크기의 정육면체 블록을 쌓아 게임 속 지형을 표현합니다. 이때, 블록이 공중에 떠 있거나, 블록 하나가 여러 개의 칸에 걸쳐 놓일 수는 없습니다. 따라서 지형을 편집하기 위해서는 각 칸의 제일 위에 블록 1개를 새로 추가하거나, 제일 위에 있는 블록 한 개를 삭제하는 방식으로 지형을 수정해야 합니다. 이때, 블록 한 개를 새로 추가하거나 삭제하기 위해서는 게임머니를 사용해야 하므로 몇 개의 블록을 추가하고 삭제할지 신중한 선택이 필요합니다.
이 게임을 즐기던 한 플레이어는 N x N 크기의 지역에 자신만의 별장을 만들고 싶어졌습니다. 이를 위해서는 울퉁불퉁한 지형의 모든 칸의 높이가 같아지도록 만들어야 합니다. 이때, 블록 한 개를 추가하려면 P의 비용이, 제거하려면 Q의 비용이 들게 됩니다.
다음은 블록 한 개를 추가할 때 5의 비용이, 제거할 때 3의 비용이 드는 경우, 3 x 3 넓이의 모든 칸의 블록 높이가 같아지도록 만드는 예시입니다.

위 그림과 같이 지형 블록이 놓여 있는 경우 모든 칸의 높이가 3으로 같아지도록 한다면 다음과 같은 모양이 됩니다.

이를 위해서는 3보다 높은 칸의 블록 2개를 제거하고, 3보다 낮은 칸에 총 8개의 블록을 추가해야 하며, 2 x 3 + 8 x 5 = 46의 비용이 들게 됩니다.
그러나 아래 그림과 같이 모든 칸의 높이가 2로 같아지도록 할 때는 6개의 블록을 제거하고, 3개의 블록을 추가하면 6 x 3 + 3 x 5 = 33의 비용이 들게 되며, 이때가 최소비용이 됩니다.

현재 지형의 상태를 나타내는 배열 land와 블록 한 개를 추가하는 데 필요한 비용 P, 블록 한 개를 제거하는 데 필요한 비용 Q가 매개변수로 주어질 때, 모든 칸에 쌓여있는 블록의 높이가 같아지도록 하는 데 필요한 비용의 최솟값을 return 하도록 solution 함수를 완성해 주세요.
제한사항
- land는 N x N 크기의 2차원 배열이며, N의 범위는 1 ≤ N ≤ 300입니다.
- land의 각 원소는 각 칸에 놓여 있는 블록의 수를 나타내며, 0 이상 10억 이하의 정수입니다.
- 각 칸에 블록 하나를 추가하는 데는 P, 제거하는 데는 Q의 비용이 들며, P, Q의 범위는 1 ≤ P, Q ≤ 100인 자연수입니다.
입출력 예
| land | P | Q | result |
| [[1, 2], [2, 3]] | 3 | 2 | 5 |
| [[4, 4, 3], [3, 2, 2], [ 2, 1, 0 ]] | 5 | 3 | 33 |
입출력 예 설명
입출력 예 #1
- 모든 땅의 높이를 1로 맞추는 데는 블록 4개를 제거해야 하므로 8의 비용이 듭니다.
- 모든 땅의 높이를 2로 맞추는 데는 블록 1개를 추가하고 블록 1개를 제거해야 하므로 5의 비용이 듭니다.
- 모든 땅의 높이를 3으로 맞추는 데는 블록 4개를 추가해야 하므로 12의 비용이 듭니다.
따라서 최소 비용은 5이므로 5를 return 합니다.
입출력 예 #2
문제의 예시와 같으며 최소 비용은 33입니다.
효율성 파트가 있는 문제입니다.
문제의 조건을 보면, N*N의 정사각형 셀로 주어져있고, 한 변의 길이는 1~300까지 가능합니다.
층은 0층부터 10억층(!!)까지 가능합니다.
이제 주어진 블록들을 0층에서 10억층까지 균일하게 만들 때,
가장 저렴한 비용으로 가능한 경우의 비용을 반환하면 됩니다.
감이 오시겠지만, 0층에서 10억층까지 일일이 계산시키면 날 샙니다.
불필요한 비용을 줄이려면,
기존 층의 최하층에서 일부러 더 파낼 필요도 없고,
기존 층의 최상층에서 일부러 더 쌓을 필요도 없습니다.
그러니까 0~10억층이 아니라, min~max층만 계산하면 됩니다.
그래도 정확성 파트의 시간초과는 면해도, 효율성은 통과하지 못 할겁니다.
(막말로 진짜 한 셀이 0층이고, 한 셀이 10억층이면..??;;)
그럼 혹시, DFS로 풀이한다면..??
우리는 어느 특정 층에 도달하는게 아니라,
비용을 줄이기만 하면 되기 때문에
맨 윗층 기준으로 이 윗층을 다 깎아내리는 것이 싼지,
맨 아랫층 기준으로 이 아랫층에 한 칸씩 더 쌓아올리는 것이 싼지 보고
더 싼대로 진행해서, 맨 윗층과 맨 아랫층이 한 층으로 만나는 점에서 멈추면 됩니다.
그러나 우리는 조이스틱 문제에서 비슷한 문제에 봉착했었습니다.
[Problem Solving/programmers] - [Lv2] 조이스틱
만약 맨 윗층을 다 깎는 비용과 맨 아랫층에 한 칸씩 더 쌓는 비용이 같다면 어느걸 선택하지?
아무거나 선택했는데 그 다음결과에서 차이가 발생하면..??
즉, 지금의 선택이 최선의 결과로 이어지질 않는다..
그럼 경우의 수에따라 무한정 호출이 늘어가고, 층 수는 이론상 0층부터 10억층까지..;;
메모리초과나 시간초과가 눈에 보이는 상황;; 이렇게는 못 풀겠죠.
풀이는 2가지로 진행합니다.
먼저, 이분탐색입니다.
이분탐색은 2로 나눠가며 원하는 부분을 찾는 방법입니다.
세로축을 비용, 가로축을 층이라고 하면, 문제의 그래프는 보통 다음의 형태 중 하나입니다.
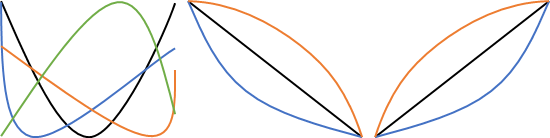
min층부터 max층까지 비용이 계속 증가하거나 감소하는 경우,
혹은 포물선의 형태로 변곡점이 생기는 경우.
우리는 어차피 비용(y축-세로축)이 제일 낮은 지점만 알면 됩니다.
처음에는 양 끝(min, max)에서 시작합니다.
이 둘의 중간값(middle = (min+max)/2)과, 그 오른쪽으로 한 칸(middle+1)의 비용을 봅니다.
middle의 비용보다 middle+1이 더 크다면,
중간부분 근처에서는 왼쪽부분이 더 작아진다는 말입니다.
전체적으로 시점을 왼쪽으로 봐야겠죠. 오른쪽끝(max)을 middle로 확 당겨옵니다.(전체 크기는 약 절반이 됩니다.)
반대로, 오른쪽부분이 더 작아진다면(middle+1이 더 작다면)
전체적으로 시점을 오른쪽으로 봐야하니, 왼쪽끝(min)을 middle+1로 확 당겨옵니다.(전체 크기는 약 절반이 됩니다.)
이렇게 반복되다가, 양 끝값이 동일한 지점을 가리킬 때
(최소비용을 찾느라 줄이고 줄이다가 겹쳐지는 순간은 그 부분이 최소비용)
그 부분이 원하는 층과 비용을 가리킬 겁니다.
0~10억 층이라도, 한 번에 5억으로 줄어들기 때문에 이분탐색은 빠르게 지점 수렴이 가능합니다.
(술게임 Up&Down의 정석 공략도 이분탐색이죠.)
한 쪽으로 계속 비용이 감소해도 그쪽으로 시점을 계속 옮기면서 언젠가 수렴하게 되며,
기울기가 -에서 +로 변하는 포물선이라도,
설령 기울기가 +에서 -로 변하는 포물선이라도 최초 정중앙이 변곡점이 아니면 오류 없이 찾아갑니다.
이 문제는 기울기가 -에서 +로 변하는데, 이 부분은 아래의 다른 풀이에서 설명됩니다.
이제, 이 부분에서의 비용을 구하기만 하면 되는데,
public long cal(int[][] land, int height, int P, int Q) {
long answer = 0;
for(int i=0;i<land.length;i++) {
for(int j=0;j<land[i].length;j++) {
if(land[i][j]>height) {
answer+=(land[i][j]-height)*Q;
}
else if(land[i][j]<height) {
answer+=(height-land[i][j])*P;
}
}
}
return answer;
}
public long solution(int[][] land, int P, int Q) {
int max = 0;
int min = Integer.MAX_VALUE;
for(int i=0;i<land.length;i++) {
for(int j=0;j<land[i].length;j++) {
if(land[i][j]>max) max = land[i][j];
if(land[i][j]<min) min = land[i][j];
}
}
int middle = 0;
while(min<=max) {
middle = (max+min)/2;
if(min==max) break;
long result1 = cal(land,middle,P,Q);
long result2 = cal(land,middle+1,P,Q);
if(result1<result2) {
max = middle;
} else if(result1==result2) break;
else {
min = middle+1;
}
}
return cal(land,middle,P,Q);
}코드 상으로는 이렇습니다만, 이대로 풀지는 못합니다.
이분탐색은 middle의 비용과 middle+1의 비용을 비교해야 하는데,
이미 middle이나 middle+1의 비용 자체가 Overflow가 발생해서 제대로 된 값 비교가 불가능합니다.
정답은 long 단위여도, 다른 구간의 비용이 long을 아득히 넘는 unsigned long이라 제대로 된 지점 탐색이 안됩니다.
그래서, 이분탐색을 비용자체가 아니라,
(height-land[i][j])*P들과 (land[i][j]-height)*Q들을 비교해서(얘들까진 long이 감당하는 듯)
해당 층에는 쌓는게 싼지, 깎는게 싼지 비교해서 구하는 방법도 있던데,
P나 Q가 한 쪽이 값이 극단적으로 크거나 했을 때 구한 지점의 주변을 다시 탐색하더라도 값이 틀어지길래 제가 다 이해하지 못하는 바 포기했습니다.
그래서 더 큰 값을 지원하는 C++로 풀어봤습니다.(이 정도 왔으면 오기가 생긴다.)
#include <vector>
using namespace std;
int n;
long long cal(vector<vector<int> >& land, int height, int P, int Q) {
long long answer = 0;
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
long long mult = height-land[i][j]>0 ? P : -Q;
answer += (long long)(height-land[i][j])*mult;
}
}
return answer;
}
long long solution(vector<vector<int> > land, int P, int Q)
{
n = land.size();
int max = land[0][0];
int min = land[0][0];
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
if(land[i][j]>max) max = land[i][j];
else if(land[i][j]<min) min = land[i][j];
}
}
int middle;
while(min<=max) {
middle = (max+min)/2;
if(min==max) break;
long long result1 = cal(land,middle,P,Q);
long long result2 = cal(land,middle+1,P,Q);
if(result1==result2) break;
else if(result1<result2) {
max = middle;
} else {
min = middle+1;
}
}
return cal(land,middle,P,Q);
}이렇게 풀면 모든 채점기준을 정말 아슬아슬하게 통과합니다.
아슬아슬한 부분은 당연히 효율성 부분인데,
cal에 참조로 넘겨준다거나, 굳이 삼항연산자를 사용하거나 해서 방법을 총 동원해서
시간을 빠득빠득 긁어모아서 통과한 경우입니다;;
그래서 이분탐색이 이 문제 풀이의 정석이 아니라는 생각이 들었습니다.
(뭐 그냥 제가 느낀 바로는.. 그냥 제 코드가 느린게 다 일수도 있지만.)
다음 풀이는 바로 이어집니다.
이번 풀이는 시간복잡도를 줄이는 방법입니다.
처음에 min~max층을 탐색하기 때문에 층 기준이었는데, 이를 셀 기준으로 바꿀겁니다.
층은 이론상 0~10억층까지 가능하지만, 셀은 1~90000개까지 밖에 있을 수 없습니다.
2D 배열(셀)을 1D 배열로 주르륵 풀어줄겁니다.
int[] blocks = new int[land.length*land.length];
for(int i=0;i<land.length;i++) {
System.arraycopy(land[i], 0, blocks, i*land.length, land.length);
}
Arrays.sort(blocks);그리고 오름차순으로 정렬하면 다음과 같은 형태를 나타낼 겁니다.
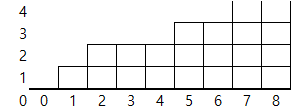
long up = 0L;
long answer = Long.MAX_VALUE;
int already = -1;
for(int i=0;i<blocks.length;i++) {
if(already!=blocks[i]) {
long down = 0L;
for(int j=i+1;j<blocks.length;j++) {
if(blocks[j]>blocks[i]) down+=(blocks[j]-blocks[i]);
}
long result = up*P + down*Q;
if(result<answer) answer=result;
already = blocks[i];
}
if(i+1<blocks.length&&blocks[i+1]>blocks[i]) up += (blocks[i+1]-blocks[i])*(i+1);
}
return answer;처음에 already는 신경쓰지 않기로 합니다.
현재 i보다 오른쪽(i+1~)의 블록들이 현재 블록의 층(blocks[i])보다 크다면, 크기차이만큼 깎아내야 합니다. 깎을 수를 down에 저장합니다.
up은 새로 쌓아올려야 할 수이기 때문에 루프의 마지막에 계산됩니다.
다음 번(i+1)으로 옮길 때, 다음 번이 층 수가 늘어난다면, up에 층수차이*이전칸들갯수만큼 쌓아야합니다.
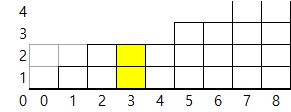
up에는 이렇게 쌓였기 때문에, 3번 인덱스 기준으로 이미 다음과 같은 상태로 봐야하고,
(0→1, 1→2로 넘어갈 때 쌓였음.)
up에는 흐릿한 블록의 수가 들어가 있습니다.
층이 같다면 굳이 루프를 반복하지 않기 위해, already에 이번 층의 수를 넣어주고,
층 수가 바뀔 때만 계산하도록 합니다.
하지만 이 풀이도 통과하지 못 합니다. 루프마다 down을 구하러 반복문이 매번 더 돌기 때문..
아직까지는 시간복잡도를 줄이는 방법을 안썼습니다. 기준만 층에서 셀로 옮겨갔을 뿐.
이제 시간 복잡도를 줄여봅시다.
long total = 0L;
for(int i=0;i<blocks.length;i++) total += blocks[i];
long prevs = 0L;
long answer = Long.MAX_VALUE;
int already = -1;
for(int i=0;i<blocks.length;i++) {
if(already!=blocks[i]) {
long up = (long)blocks[i]*i-prevs;
long down = total-prevs-(long)(blocks.length-i)*blocks[i];
long result = up*P + down*Q;
if(result<answer) answer=result;
already = blocks[i];
}
prevs += blocks[i];
}
return answer;반복문을 시작하기 전에, 전체 블록수(total)를 세어줍니다.

total이 가리키는건 저 연녹색부분이 될 겁니다. 감이 오겠지만 down을 직접 구하는 대신 사용할 상수입니다.
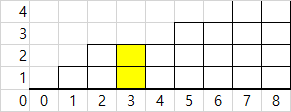
이해를 돕기 위해, 루프가 진행된 상태의 i=3에서 살펴보겠습니다.
루프의 마지막에 보면 prevs에 이전까지의 블록 수를 쌓고있는걸 볼 수 있습니다.
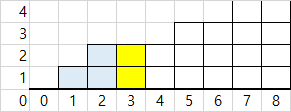
prevs는 여기 하늘색으로 표시된 부분일 겁니다.
즉, up은 (현재블록층*i)-이전블록들을 하면, 새로 쌓을 부분이 구해집니다.
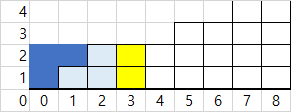
이제 long up = (long)blocks[i]*i-prevs;은 이해가 되셨을겁니다.
이제 down을 구해야하는데,
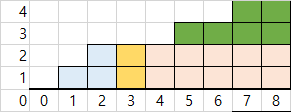
이전에 total에 모든 블록들을 집어넣었었습니다.
여기에서 당연히 prevs(하늘색)는 빼야할테고..
셀의 총 수(여기선 9)-i를 하면, 자신과 오른쪽 모두의 셀 수(9-3=6)가 됩니다.
이 셀 수에 현재층을 곱하면 연홍색(자기자신포함)부분이 됩니다.
total에서 연홍색부분과 하늘색 부분을 빼주면, 깎아낼 부분(녹색)이 됩니다.
long down = total-prevs-(long)(blocks.length-i)*blocks[i];
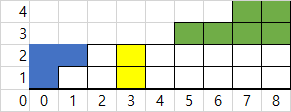
딱히 추가반복문을 사용하지 않고도 쌓을 부분과 깎을 부분을 구했습니다.
위의 풀이에서 언급했듯, 층 수가 같으면 결과는 같으니 already로 불필요한 반복을 피합니다.
문제의 처음에서, 그래프는 다음의 형태 중 하나라고 말했었습니다.

세로축(y)이 비용이고, 가로축(x)이 층이 됩니다.
맨 아래식을 통해 볼까요.
long up = (long)blocks[i]*i-prevs;
long down = total-prevs-(long)(blocks.length-i)*blocks[i];
long result = up*P + down*Q;block[i]가 현재 층(x)이 될테죠.
y = up*P + down*Q
y = (x*i-prevs)*P + (total-prevs-(N^2-i)*x)*Q
total은 이 문제 안에서 변하지 않는 상수가 될겁니다.(T)
N^2 역시 이 문제 안에서 변하지 않는 상수가 될겁니다.(N')
y = (x*i-prevs)*P + (T-prevs-(N'-i)*x)*Q
x는 층 수이고, i는 단지 셀의 index입니다.
우리는 같은 층 수에 대해서는 i가 다르더라도 반복계산을 하지 않았습니다.(결과가 같기에)
i의 의미는 up을 위해 현재 층 기준 왼쪽의 셀들 수를 셀 때와 down을 위해 오른쪽의 셀들 수를 셀 때에 있습니다.
i가 증가할 때마다 prevs에 이전 블록들을 쌓아왔기 때문에 i를 기준으로 파란부분을 구한 것이고..
정확한 형태는 몰라도
i는 ax+C1으로,
prevs는 bx+C2로 표현이 가능합니다.
(위 식들이 1차식이 아니라 2차식 이상일 수도 있지만, 상관없습니다. a가 중요하기 때문.)
y = (x*(ax+C1)-bx+C2)*P + (T-bx-C2-(N'-ax-C1)*x)*Q
y = (a*P)x^2 + (C1*P)x - (b*P)x + C2*P + T*Q - (b*Q)x - C2*Q - (N'*Q)x + (a*Q)x^2 + (C1*Q)x
y = (a*(P+Q)) x^2 + ((C1-b)*P-(b+N'-C1)*Q) x + C2*(P-Q) + T*Q 로,
y = A x^2 + B x + C 의 형태가 되네요. 이게 경우에 따라 곡선으로, 또는 직선이 되기도 하겠죠.
(가정한 식의 차수가 높으면 더 높은 차수형태가 되겠지만..)
기울기(A)인 (a*(P+Q))에 대해서는, P와 Q는 1 이상 100이하의 양수로 주어졌고,
a는 층이 증가함에 따라 i가 증가했으면 증가했지 감소하진 않으므로 양수임을 알 수 있습니다.
즉, 변곡점을 지녔다해도 기울기가 -에서 +인 곡선만 나올겁니다. 녹색 그래프는 이제 생각하지 않아도 되겠네요.
(그러면 result가 answer(이전 계산)보다 커진다면 미련없이 break로 빠져나와도 되겠습니다.)
'Problem Solving > programmers' 카테고리의 다른 글
| [Lv1] 두 개 뽑아서 더하기 (0) | 2021.04.12 |
|---|---|
| [Lv4] 스마트한 프로도 (0) | 2019.05.02 |
| [Lv3] 보행자 천국 (0) | 2019.04.25 |
| [Lv3] 가장 먼 노드 (0) | 2019.04.25 |
| [Lv5] 블록 게임 (0) | 2019.04.24 |
잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -



