잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -
현록의 기록저장소
[Lv3] 하노이의 탑 본문
https://programmers.co.kr/learn/challenges
프로그래밍 강의 | 프로그래머스
기초부터 차근차근, 직접 코드를 작성해 보세요.
programmers.co.kr
문제 설명
하노이 탑(Tower of Hanoi)은 퍼즐의 일종입니다. 세 개의 기둥과 이 기동에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있습니다. 게임의 목적은 다음 두 가지 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓는 것입니다.
- 한 번에 하나의 원판만 옮길 수 있습니다.
- 큰 원판이 작은 원판 위에 있어서는 안됩니다.
하노이 탑의 세 개의 기둥을 왼쪽 부터 1번, 2번, 3번이라고 하겠습니다. 1번에는 n개의 원판이 있고 이 n개의 원판을 3번 원판으로 최소 횟수로 옮기려고 합니다.
1번 기둥에 있는 원판의 개수 n이 매개변수로 주어질 때, n개의 원판을 3번 원판으로 최소로 옮기는 방법을 return하는 solution를 완성해주세요.
제한사항
- n은 15이하의 자연수 입니다.
입출력 예
| n | result |
| 2 | [ [1,2], [1,3], [2,3] ] |
입출력 예 설명
입출력 예 #1
다음과 같이 옮길 수 있습니다.


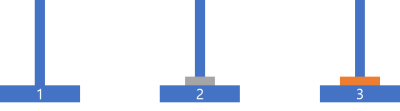
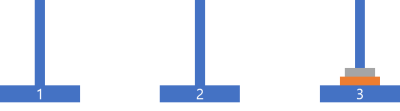
그 유명한 하노이의 탑입니다.
기본 문제라 기둥은 3개로 기본으로 나왔습니다.
문제에서는 원기둥의 숫자로 출발지,도착지를 배열들로 담으라고 했지만,
실제로 구현하려면 Stack을 이용하면 됩니다.
public void write(int[][] answer, int origin, int target) {
for(int i=0;i<answer.length;i++) {
if(answer[i][0]==0) {
answer[i][0]=origin;
answer[i][1]=target;
return;
}
}
}
public void hanoi(int n, int[][] answer, int origin, int spare, int target) {
if(n==1) {
write(answer,origin,target);
} else {
hanoi(n-1,answer,origin,target,spare);
write(answer,origin,target);
hanoi(n-1,answer,spare,origin,target);
}
}
public int[][] solution(int n) {
int[][] answer = new int[(int)Math.pow(2, n)-1][2];
hanoi(n, answer, 1, 2, 3);
return answer;
}
코드 자체는 간단합니다.
3기둥의 경우 과정은 2^(원판수)-1의 과정으로 진행됩니다.
write함수는 단순히 기록용 함수라 신경쓰지 않아도 됩니다.
하노이의 탑은 재귀를 반복하면서 이루어집니다.
하노이의 탑에서 3개의 탑은
"원본", "빈 탑", "최종목적지(빈 탑)"이 되는데,
"원본", "도우미" "목적지"로 생각됩니다.
지금 원하는 n판을 목적지로 옮기기 위해 나머지 위의 애들을 도우미로 옮겨두고 n판은 목적지로 갈 수 있습니다.
우선 간단하게 3탑 3판 과정을 봅니다.
1
2
3
<1> <2> <3>
"3"은 <3>으로 갈테니, "2"에게 <2>로 비켜났다가 따라서 <3>으로 오라고 합니다.
2
3 1
<1> <2> <3>
"2"는 <2>로 갈테니, "1"에게 <3>으로 비켜났다가 따라서 <2>로 오라고 합니다.
"1"은 <3>으로 잠시 비켜났습니다.
3 2 1
<1> <2> <3>
이제 "2"가 <2>로 비켜날 수 있습니다.
1
3 2
<1> <2> <3>
"1"은 아까 비켜났다가 따라오라고 했어서 <2>로 따라왔습니다.
1
2 3
<1> <2> <3>
"3"은 이제 목적지인 <3>으로 이동했습니다.
1 2 3
<1> <2> <3>
"2"는 "3"이 따라오랬어서 <3>으로 가려고 했는데, "1"이 막고 있습니다.
그래서 "1"에게 <1>로 비켜났다가 따라서 <3>으로 오라고 합니다.
2
1 3
<1> <2> <3>
"2"는 이제 목적지인 <3>으로 이동했습니다.
1
2
3
<1> <2> <3>
"1"은 "2"가 따라오랬어서 <3>으로 이동했습니다.
위 과정을 보면 알겠지만,
n판이 목적지로 가기 위해서는 자기 바로 위의 판에게 "목적지<3>가 아닌 다른판<2>"에 갔다가 "목적지<3>"에 너도 와라고 명령합니다.
그 윗판 입장에서는 자신의 목적지는 <2>가 되고, <2>로 바로 갈 수 있으면 가고, 아니면 또 윗판에게 <3>으로 비켜났다가 <2>로 따라와라고 명령합니다.
즉 판이 위에 있다면 목적지와 도우미가 바뀌면서 명령이 전달되고,
단순히 비켜나는 것이 아니라 도우미로 비켰다가 내가 향할 곳에 너도 와라가 됩니다.
그렇게 해야 최종목적지에 다시 쌓이니까요.
또한, 하노이의 탑은 아무리 복잡해도 두 단계로만 생각하면 된다고 합니다.
1~7까지의 판이 <1>에 있고, <3>까지 옮기는 것이 목적이라면,
1~6을 <2>에 옮기고 / 7을 <3>에 옮기는 것이라고.
여기서 1~6이 <2>에 있고, <3>까지 옮기는 것이 목적이라면,
1~5를 <1>에 옮기고 / 6을 <3>에 옮기는 것이라고.
여기서 1~5가 <1>에 있고, <3>까지 옮기는 것이 목적이라면,
1~4를 <2>에 옮기고 / 5를 <3>에 옮기는 것이라고.
여기서 1~4가 <2>에 있고, <3>까지 옮기는 것이 목적이라면,
1~3을 <1>에 옮기고 / 4를 <3>에 옮기는 것이라고.
여기서 1~3이 <1>에 있고, <3>까지 옮기는 것이 목적이라면,
1~2를 <2>에 옮기고 / 3을 <3>에 옮기는 것이라고.
여기서 1~2가 <2>에 있고, <3>까지 옮기는 것이 목적이라면,
1을 <1>에 옮기고 / 2를 <3>에 옮기는 것이라고.
이제 1을 <3>으로 옮기면 끝.
위 과정을 보면 n판을 <3>으로 옮기기 위해, 그 윗판들을 <2>와 <1>로 번갈아 가면서 옮기게 됩니다. 이게 도우미 탑이 자꾸 바뀌는 원인이죠.(윗판들이 우르르 <1>과 <2>로 바뀌니(원본), 목적지는 <3>고정이고 남는 탑이 자꾸 나머지탑이 되니까)
설명을 아래에서 위로 올라가면서 n만 늘리면 3탑은 무한정 이 과정으로 이루어집니다.
(4탑부터는 빈 타워가 늘어나니까 과정은 달라지지만 원리는 같습니다.)
코드를 다시 보면,
public void hanoi(int n, int[][] answer, int origin, int spare, int target) {
if(n==1) {
옮긴다(answer,origin,target);
} else {
hanoi(n-1,answer,origin,target,spare);
옮긴다(answer,origin,target);
hanoi(n-1,answer,spare,origin,target);
}
}n이 1이 되기 전까진 무한정 윗판에 n-1하면서 target과 spare가 바뀌면서 명령을 전달합니다.
n이 2인 입장에서 보면,
n=1에게 spare로 비껴나라.
내가 target으로 가고,
n=1에게 target으로 따라와라.
가 됩니다.
n이 3인 입장에서 보면,
n=2에게 spare로 비껴나라.(이 한줄이 위의 3줄)
내가 target으로 가고,
n=2에게 target으로 따라와라.(이 한줄이 또 위와 비슷한 3줄로 실행되겠죠.)
가 됩니다.
이 부분은 재귀함수의 호출과 반환 순서만 이해하시면 금방 이해되실 겁니다.
Stack을 이용한 실행용 함수도 첨부합니다.
public class Hanoi {
static class Top {
char index;
Stack<Integer> stack;
public Top(char index) {
this.index = index;
this.stack = new Stack<>();
}
}
static Top t1;
static Top t2;
static Top t3;
public static void move(int n, Top origin, Top target) {
System.out.println("----------\n"+n+"을 "+origin.index+"에서 "+target.index+"으로");
target.stack.push(origin.stack.pop());
System.out.println(t1.stack+"/"+t2.stack+"/"+t3.stack);
}
public static void hanoi(int n, Top origin, Top spare, Top target) {
if(n==1) {
move(n, origin, target);
} else {
hanoi(n-1,origin,target,spare);
move(n, origin, target);
hanoi(n-1,spare,origin,target);
}
}
public static int[][] solution(int n) {
t1 = new Top('A');
t2 = new Top('B');
t3 = new Top('C');
for(int i=n;i>=1;i--) {
t1.stack.push(i);
}
System.out.println(t1.stack+"/"+t2.stack+"/"+t3.stack);
hanoi(n, t1, t2, t3);
return new int[2][2];
}
public static void main(String[] args) {
solution(3);
}
}[3, 2, 1]/[]/[]
----------
1을 A에서 C으로
[3, 2]/[]/[1]
----------
2을 A에서 B으로
[3]/[2]/[1]
----------
1을 C에서 B으로
[3]/[2, 1]/[]
----------
3을 A에서 C으로
[]/[2, 1]/[3]
----------
1을 B에서 A으로
[1]/[2]/[3]
----------
2을 B에서 C으로
[1]/[]/[3, 2]
----------
1을 A에서 C으로
[]/[]/[3, 2, 1]
'Problem Solving > programmers' 카테고리의 다른 글
| [Lv5] 오픈채팅방 (0) | 2019.04.24 |
|---|---|
| [Lv3] 숫자 게임 (1) | 2019.04.23 |
| [Lv3] 최고의 집합 (0) | 2019.04.23 |
| [Lv3] 줄 서는 방법 (0) | 2019.04.23 |
| [Lv3] 방문 길이 (0) | 2019.04.22 |
잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -

