잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -
현록의 기록저장소
[Lv1] 소수의 합, 소수 찾기 본문
https://programmers.co.kr/learn/challenges
프로그래밍 강의 | 프로그래머스
기초부터 차근차근, 직접 코드를 작성해 보세요.
programmers.co.kr
문제 설명
2부터 N까지의 모든 소수의 합을 구하세요.
N이 7이라면 {2,3,5,7} = 17을 출력 하시면 됩니다.
N의 범위는 2이상 10,000,000이하 입니다.
효율성 테스트의 모든 시간 제한은 1초입니다.
문제 설명
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
제한 조건
- n은 2이상 1000000이하의 자연수입니다.
입출력 예
| n | result |
| 10 | 4 |
| 5 | 3 |
입출력 예 설명
입출력 예 #1
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
입출력 예 #2
1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환
소수는 자신보다 작은 두 개의 자연수를 곱하여 만들 수 없는 1보다 큰 자연수이다. (2,3,5,7,...)
유클리드의 정리에 의해 소수는 무한하다고 한다.
https://ko.wikipedia.org/wiki/%EC%86%8C%EC%88%98_(%EC%88%98%EB%A1%A0)
소수 (수론) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 좌측은 소수, 우측은 합성수. 소수란 자신보다 작은 두 자연수를 곱하여 만들 수 없는 1보다 큰 자연수이다. 소수(素數, 발음: [소쑤], 문화어: 씨수, 영어: prime number)는 자신보다 작은 두 개의 자연수를 곱하여 만들 수 없는 1보다 큰 자연수이다. 예를 들어, 5는 1x5 또는 5x1로 수를 곱한 결과를 적는 유일한 방법이 그 수 자신을 포함하기 때문에 5는 소수이다. 그러나 6은 자신보다 작은 두 숫자
ko.wikipedia.org
소수를 구하기 위해서는 그 수가 1과 자신으로 밖에 딱 나뉘어지지 않아야 한다.(나머지가 0이어야 한다.)
이론상으로는 113이 소수인지 확인하려면 2부터 112까지 113을 나누어보려 했을 때 모두 나머지가 발생해야 한다.
물론 코드로 구현할 순 있겠지만 수가 클 수록 처리속도는 느려진다.
어떤 수가 소수인지 판별하기 위한 가장 효율적인 방법 중 하나인 에라토스테네스의 체를 이용하면 속도를 획기적으로 줄일 수 있다.
에라토스테네스의 체 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 둘러보기로 가기 검색하러 가기 수학에서 에라토스테네스의 체는 소수(소쑤)를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다. 알고리즘[편집] 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색) 자기 자신을 제외한 2의 배수를 모두 지운다. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초
ko.wikipedia.org
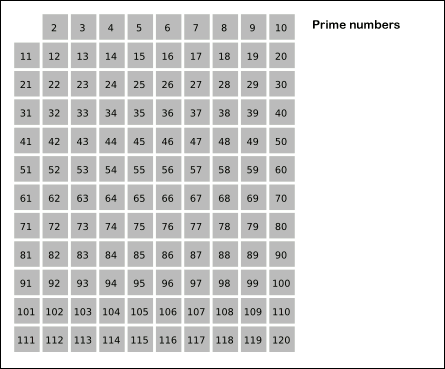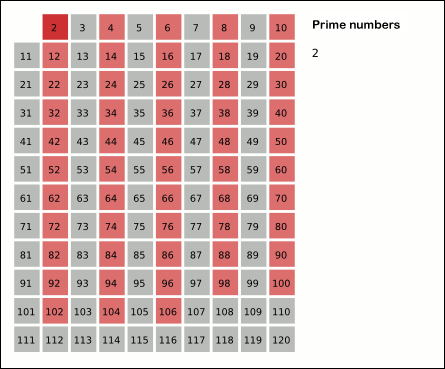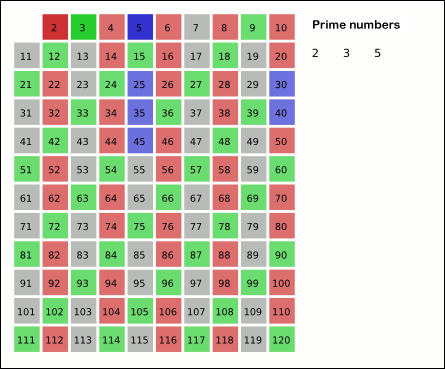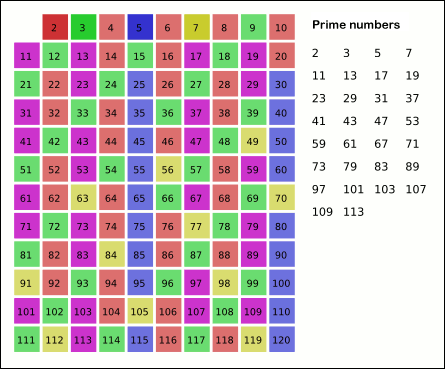
에라토스테네스의 체를 간단하게 설명하자면, 2부터 120(N)까지의 수 중 소수가 아닌 수를 제거해 나가는 것이다.
가장 처음에 2를 소수로 빼두고, 2의 배수(4,6,8,10,..)는 지워버린다.(2로 나뉘어지니까 소수가 아님.)
살아있는 수 중 다음 수인 3을 소수로 빼두고, 그 배수(6(이미 지워졌지만), 9, 12, 15,...)는 지워버린다.
살아있는 수 중 다음 수인 5를 소수로 빼두고,...
를 반복하는데, 120(N)의 제곱근까지만 행하면 나머지는 모두 소수라고 한다.
즉, 120의 루트값인 10.9545의 정수값인 10까지만 하면 되는 것이다.
소수의 집합을 생각해보려면,
int N = 120;
boolean[] numbers = new boolean[N];여기에서 1~120개의 true/false 여부가 생성된다.
초기값인 false 그대로라면 소수로 인정받아 남았다고 생각하고, true라면 지워진 것으로 생각한다.
numbers[0] = true;1은 소수가 될 수 없으니 바로 지워버린다.
int max = (int)Math.sqrt(N);혹은
int max = (int)sqrt(N);로 계산 최댓값을 정해준다. (N=120이면 max=10)
for(int i=2;i<=max;i++) {
for(int j=i*2;j<=N;j+=i) {
numbers[j-1] = true;
}
}2부터 max까지만 검사할텐데,
검사 해당 수는 건너 뛰고(소수로 남겨두고),
그 배수들 (i*2) 부터 지워나가며,
증가는 i만큼 더해준다.(i*2, i*3, i*4, ... 로 i는 패스하고 i의 배수들만 착실히 지워나감.)
그러다 j가 N까지만 검사하면 되므로, j<=N으로 한계를 정한다.
첫 문제에서 N까지의 모든 소수의 합을 구하라고 했으니,
long answer = 0;
for(int i=1;i<numbers.length;i++) {
if(!numbers[i]) answer+=(i+1);
}
return answer;어차피 0번째인 1은 소수가 아님을 알고 있으니..
1번째인 2부터 초기값인 false로 남아있는 애들만 더해준다.
두번째 문제에서는 소수의 갯수를 구하라고 했으니,
int answer = 0;
for(int i=1;i<numbers.length;i++) {
if(!numbers[i]) answer++;
}
return answer;
여기까지가 소수하면 단골이자 기본인 에라토스테네스의 체 활용과 나머지 풀이.
'Problem Solving > programmers' 카테고리의 다른 글
| [Lv2] 스킬트리 (0) | 2019.04.11 |
|---|---|
| [Lv2] 주식가격 (0) | 2019.04.10 |
| [Lv1] 최대공약수와 최소공배수 (0) | 2019.04.10 |
| [Lv1] 2016년 (0) | 2019.04.10 |
| [Lv1] 체육복 (0) | 2019.04.10 |
잘못된 정보가 있다면, 꼭 댓글로 알려주세요(비로그인 익명도 가능).
여러분의 피드백이 저와 방문자 모두를 올바른 정보로 인도할 수 있습니다.
감사합니다. -
